Note these techniques are applicable to all graphs, including binary trees.
Adjacency lists
A convenient way to represent the a nodes edges, and hence connected nodes, is to use an adjacency list. We can then construct our graph like so:

As you can see, the adjacency list is simply the graph itself (here I use the index to represent the graph, but a map would also work) and a list of its connected nodes.
Depth first search
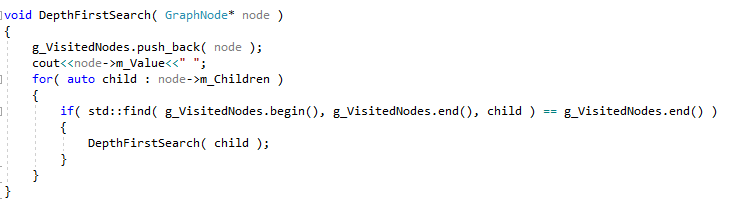
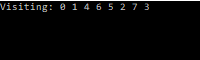
Here, the goal is to start searching from the outer extremeties of the graph first. One approach is to recurse through a nodes children, and its children’s children, and track who we have visited.

Breadth-first search
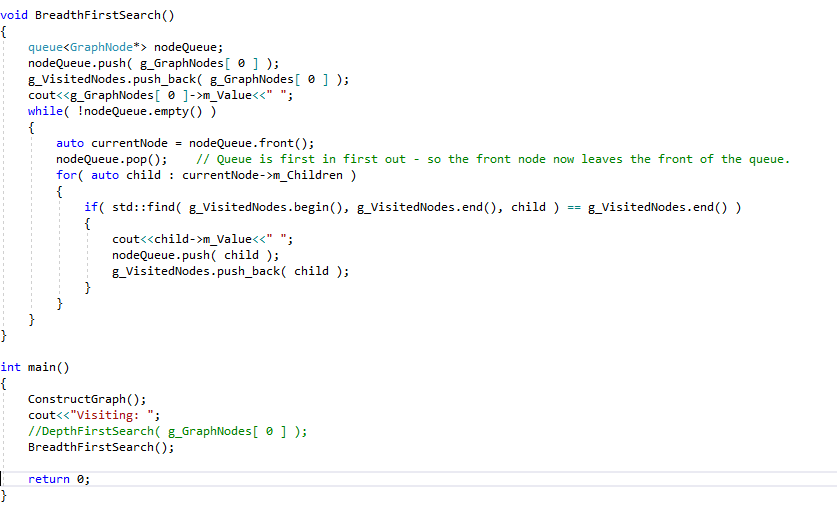
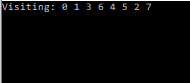
Here, we want to search neighbouring nodes first. It is convenient here to use a queue, this allows us to maintain the order of a our node’s children as we search through and compile our list of children. We pop the current node off the queue, and then add its children to our queue as we search them.
Depth-first search: Stack vs Queue
Note that if we take a similar code structure to the above algorithm, but instead we used a stack, and exploited its last-in first-out principle, as opposed to a queue’s first-in first-out mechanism, we achieve an alternative non-recursion form of a depth-first search.