My solution to BinaryGap provides a straight forward way to determine if an integer is a power of two: by looping through its binary representation there should be only one ‘1’. But is there a way to determine this without looping?

Solution 1: Decrement and compare

If you are familiar with subtracting binary numbers from each other, then you will know that the lone ‘1’ bit in a power of two is replaced by a ‘0’ and all lower bits become ‘1’. Therefore if a number is not zero and is a power of two, by taking the bitwise AND of x and (x-1), we should get zero, as illustrated below:

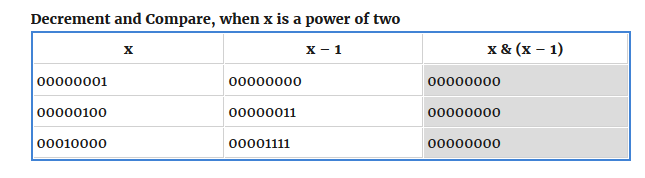
if( ( 0 != x ) &&  0 == ( x & ( x-1 ) ) ){ return true }

Solution 2: Complement and compare
Two’s complement means to take the complement of a number and then add one. It is used to represent integers and their negative equivalents without incorrectly representing zero as a negative that can happen with one’s complement.
Therefore if a non-zero number is a power of two, then the bitwise AND of a number x and it’s twos complement (~x+1) representation will equal the original number x.

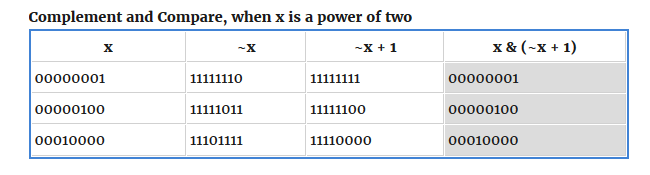
This is because, as shown in the above table, the arithmetic of adding 1 to a power of two’s complement shifts all numbers below the lone ‘1’ bit which will be ‘0’ after taking the complement to zero and putting the bit back to ‘1’ again.

if( ( 0 != x ) && x == ( x & (~x + 1 ) ) ){ return true; }

Source: Ten ways to check whether a number is a power of two in C