Frog Jump

A small frog wants to get to the other side of the road. The frog is currently located at position X and wants to get to a position greater than or equal to Y. The small frog always jumps a fixed distance, D. You must count the minimal number of jumps that the small frog must perform to reach its target.

Assume that:

X, Y and D are integers within the range [1..1,000,000,000];

• X ≤ Y.

Complexity:

• expected worst-case time complexity is O(1);
• expected worst-case space complexity is O(1).

Suboptimal solution

Seem easy right? You put this in a loop and add D until the number of steps >= Y as follows:
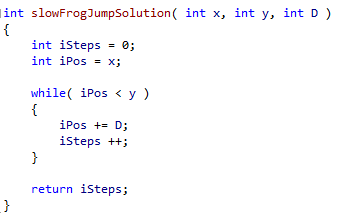Except that the exercise requests a time complexity of O(1). That is one operation. The above is in O(Y-X) time complexity and will only award you with a score of 55%.

Note: The above however can be a useful way of testing that your O(1) solution is correct. This can be useful considering that Codility will use at least 8 test cases to stress test your solution.

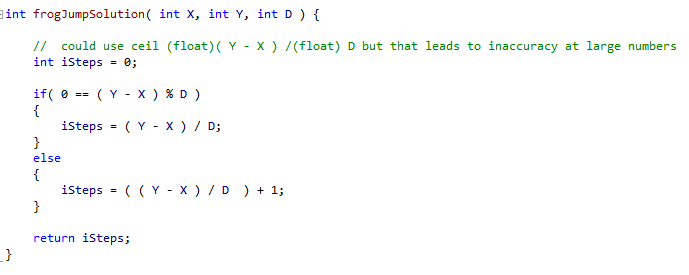
O(1) solution

We use a bit of arithmetic: ( Y – X ) / D. If that is a whole number (modulus = 0) then that will suffice. Otherwise we find the ceiling of the integer by adding 1.

You may get away without this by casting to a float, but that leads to a suboptimal solution due to floating point error.